Maple là một trong những phần mềm giải toán chuyên nghiệp hàng đầu. Nó có khả năng giải quyết hầu hết các dạng toán từ tiểu học đến đại học, bao gồm các lĩnh vực như số học, đại số, hình học, giải tích, và nhiều hơn nữa.
Trong bài viết này, mình sẽ tập trung vào việc hướng dẫn các lệnh và các dạng toán thường gặp trong chương trình trung học. Bạn có thể truy cập trang chủ của nhà sản xuất để tìm hiểu thêm về các lệnh khác. Bây giờ, mình sẽ bắt đầu hướng dẫn cách sử dụng phần mềm Maple để giải các bài tập đại số thường gặp.
Các phép toán cần được thực hiện trong môi trường toán học Math. Nếu bạn đang ở trong môi trường soạn thảo Text, hãy chọn biểu tượng [> trên thanh công cụ chuẩn trước khi nhập lệnh.
Khi đó, trước mỗi lệnh bạn nhập sẽ có dấu lớn màu nâu như hình dưới đây.
Bạn có thể nhập trực tiếp các lệnh vào chương trình hoặc sử dụng thẻ Expression để nhập, rất thuận tiện, đặc biệt khi bạn mới bắt đầu sử dụng chương trình.

I. Các phép toán và ký hiệu toán học
Mỗi lệnh đều được mình trình bày cú pháp và ví dụ minh họa (ngoại trừ các lệnh quá đơn giản) ngay bên dưới để bạn có thể dễ dàng thực hành.
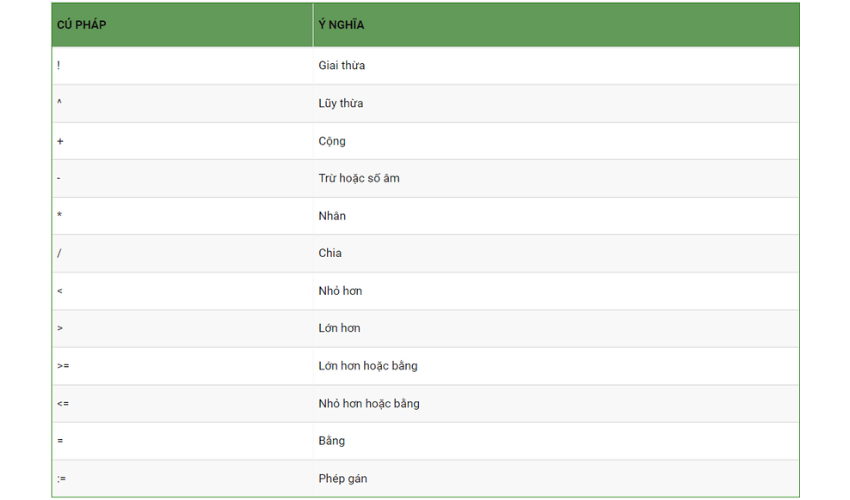
Các phép toán và ký hiệu toán học trong chương trình Maple tương tự như trong ngôn ngữ lập trình Pascal. Tổng cộng, chúng ta có 12 phép toán và ký hiệu phép toán.
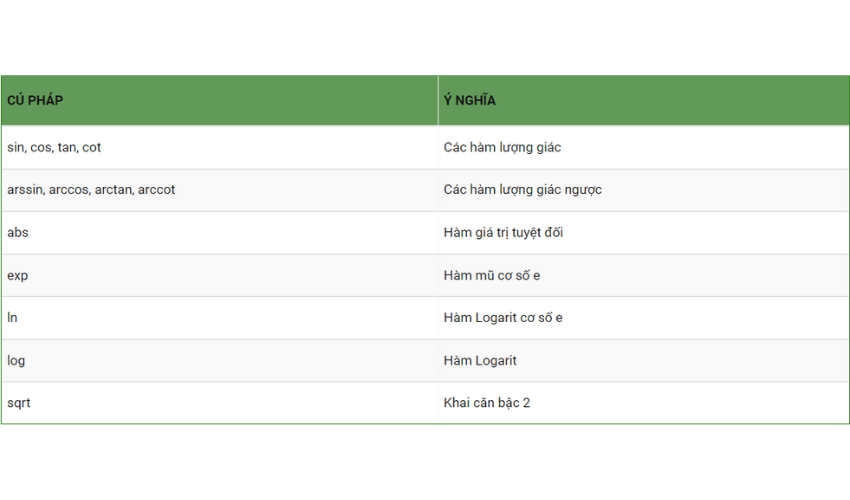
II. Các hàm phổ biến trong Maple
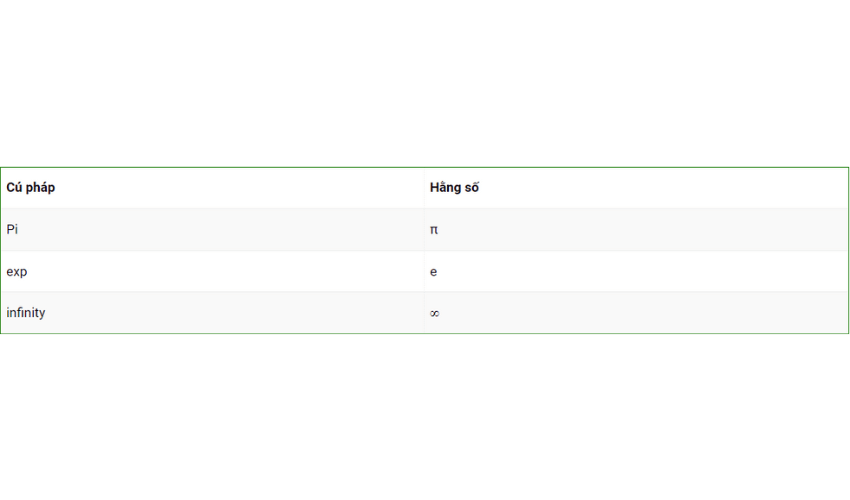
III. Các hằng số phổ biến trong Maple
IV. Các phép tính số học trong Maple
#1. Các phép toán cơ bản
1.1. Bốn phép toán cơ bản (cộng, trừ, nhân, chia)
4+5;
7-5;
8*5;
15/5;
1.2. Phép lũy thừa
5^2;
6^5;
1.3. Phép khai căn
sqrt(18);
sqrt(124);
5*6^(1/2);
#2. Thứ tự thực hiện các phép toán trong Maple
Trong Maple, các phép toán sẽ được xử lý theo thứ tự ưu tiên mặc định như sau: trước tiên là lũy thừa, sau đó là khai căn, tiếp theo là nhân, chia, cộng và trừ.
Để Maple biết phép toán nào cần ưu tiên thực hiện trước, bạn cần đặt chúng trong cặp dấu ngoặc đơn.
#3. Phép tính với số nguyên
3.1. Bội chung nhỏ nhất của 2 hay nhiều số
Để tìm bội chung nhỏ nhất của 2 số a và b, ta dùng lệnh lcm(a, b);
Ví dụ: lcm(20,60);
Để tìm bội chung nhỏ nhất của 3 số a, b, và c, ta dùng lệnh lcm(lcm(a, b), c);
Ví dụ: lcm(lcm(9,8),62);
3.2. Ước chung lớn nhất
Để tìm ước chung lớn nhất của 2 số a và b, ta dùng lệnh gcd(a, b);
Ví dụ: gcd(1800,2016);
Để tìm ước chung lớn nhất của 3 số a, b, và c, ta dùng lệnh gcd(gcd(a, b), c);
Ví dụ: gcd(gcd(100,20),50);
3.3. Phân tích một số ra thừa số nguyên tố
Để phân tích số nguyên a ra thừa số nguyên tố ta dùng lệnh ifactor(a);
Ví dụ: ifactor(2505004); ifactor(2^12+1);
3.4. Kiểm tra số n có phải số nguyên tố hay không
Để kiểm tra một số n có phải số nguyên tố hay không ta dùng lệnh isprime(n);
Ví dụ: isprime(7); isprime(15);
3.5. Tìm số nguyên tố đứng trước hoặc sau số tự nhiên
Để tìm số nguyên tố đứng trước số tự nhiên n ta dùng lệnh prevprime(n);
Ví dụ: nextprime(2015);
3.6. Tìm nghiệm nguyên của phương trình hoặc hệ phương trình
Để tìm nghiệm nguyên của phương trình ta dùng lệnh isolve(phương trình,{tham số}); trong đó tham số là các số để máy biểu thị nghiệm của phương trình
Ví dụ: isolve(3*x+7*y=9,{t,u});
Để tìm nghiệm nguyên của hệ phương trình ta dùng isolve({phương trình 1, phương trình 2, …}, {tham số});
Ví dụ: isolve({x+y-z=0,3*x-9*y+10*z=10},{t,u,v});
Hình
3.7. Tìm thương hoặc dư của phép chia
Để tìm thương của phép chia a cho b ta dùng lệnh iquo(a,b);
Ví dụ: iquo(125,6);
Để tìm phần dư của phép chia a cho b ta dùng lệnh irem(a,b);
Ví dụ: irem(125,6);
3.8. Giải phương trình module
Để giải phương trình theo modul p trong Z ta dùng lệnh msolve(phương trình, p);
Ví dụ: msolve(3*x+y=10, 10);
Để giải hệ phương trình theo modul p trong Z ta dùng lệnh msolve({phương trình 1, phương trình 2,…}, p);
Ví dụ: msolve({3*x+y=10,y=9}, 10);
#4. Phép tính với các số thập phân với phần mềm Maple
4.1. Tính giá trị gần đúng của một biểu thức
Để tính giá trị gần đúng của một biểu thức có k chữ số ta dùng lệnh evalf(biểu thức, k);
Tính giá trị biểu thức đến 6 số thập phân:
Ví dụ: evalf(Pi^2-Pi^3,6);
Chú ý: chữ Pi phải viết chữ P hoa.
4.2. Đơn giản biểu thức
Để đơn giản biểu thức f ta dùng lệnh simplify(f);
Ví dụ: simplify(sqrt((2+sqrt(3))/(2-sqrt(3)))+sqrt((2-sqrt(3))/(2+sqrt(3))));
4.3. Tìm số lớn nhất hoặc số nhỏ nhất
Để tìm số lớn nhất hoặc nhỏ nhất trong các số a, b, c,…ta dùng lệnh max(a,b,c,…); hoặc min(a,b,c,…);
Ví dụ:
max(2^9,9^2);
min(2^9,9^2);
4.4. Tính giá trị nhỏ nhất hoặc lớn nhất của một biểu thức
Để tìm giá trị lớn nhất hoặc nhỏ nhất của một biểu thức ta dùng lệnh maximize(biểu thức, khoảng chạy); hoặc minimize(biểu thức, khoảng chạy);
Ví dụ: maximize(sin(x)+2,x=0..Pi); minimize(cos(x)+sin(x),x=0..Pi);
4.5. Giải phương trình hoặc hệ phương trình
Để giải phương trình hoặc hệ phương trình ta dùng lệnh isolve(phương trình, biến); hoặc isolve({phương trình 1, phương trình 2,…},{x,y,…});
Ví dụ:
solve(x^2-3*x+2=0,{x});
solve({x+y=3,2*x-y=0},{x,y});

#5. Phép tính với đa thức
5.1. Cộng, trừ, nhân, chia đa thức
Các phép toán cộng, trừ, nhân, chia đa thức trong Maple tương tự như các phép toán tương ứng trong toán học thông thường. Tuy nhiên, có một vài điểm cần lưu ý như sau:
Giữa các hệ số và biến phải có dấu * tức là để đánh 5x thì ta phải nhập 5*x.
Nếu kết quả của phép toán không như mong muốn, chúng ta có thể sử dụng các lệnh phù hợp để điều chỉnh định dạng kết quả theo ý muốn.
(12*x^2+9*x-10)+(20*x-50*x^3+7*x^2-2015);
(12*x^2+9*x-10)-(20*x-50*x^3+7*x^2-2015);
(x^3+10-8*x^4)*(x^2+9-20*x^7);
(x^4+x^2-9)/(x+1);
(x+4+x^2)^3;
5.2. Đơn giản đa thức
Để đơn giản đa thức f ta dùng lệnh simplify(f);
Ví dụ: simplify(x^4+x^5-6*x^7+30*x^4+x^2-10*x-50*x^3+70*x^2-100*x^4);
5.3. Khai triển một đa thức
Để khai triển đa thức f ta dùng lệnh expand(f);
Ví dụ: expand((x^3+6*x+9)^3);
5.4. Tìm phần dư và thương của phép chia đa thức
Để tìm thương của phép chia đa thức f cho g ta dùng lệnh quo(f,g,x);
quo((x^4+x^3-x+2),(x+1), x);
Để tìm dư của phép chia f cho g ta dùng lệnh rem(f,g,x);
rem(((x^4+x^3-x+2),(x+1), x));
5.5. Tìm giá trị của đa thức tại một giá trị
Để tìm giá trị của đa thức f khi x=k(t) thì ta dùng lệnh subs(x=k(t), f);
Ví dụ:
f:=subs(x=5*t+1,x^5+7*x-10);
subs(t=2,f);
5.6. Phân tích một đa thức thành nhân tử
Để phân tích một đa thức f thành nhân tử ta dùng lệnh factor(f);
Ví dụ:
factor(x^4+2*x^2+1);
factor(a^2*(b-c)+b^2*(c-a)+c^2*(a-b));
factor(x^6-6*x^4-4*x^3+9*x^2+12*x+4);
5.7. Tìm hệ số của đa thức
Để tìm hệ số của xn trong đa thức f ta dùng lệnh coeff(f,x,n);
Ví dụ: coeff((3*x^2-3*x+2)^2,x,3);
5.8. Tìm bậc của đa thức
Để tìm bậc của đa thức f ta dùng lệnh degree(f,x);
Ví dụ: degree(x^7+x^5*(x^2+1)-(x-2)^4*(x^6-8));
5.9. Sắp xếp hệ số của đa thức dưới dạng tổng các lũy thừa
Để sắp xếp các hệ số của đa thức f dưới dạng tổng các lũy thừa ta dùng lệnh collect(f,x);
Ví dụ: collect(x^3+a^2*x-x^2+5*x+x^4-9*b*x^2,x);
5.10. Sắp xếp đa thức theo chiều tăng dần lũy thừa của biến
Để sắp xếp đa thức f theo chiều tăng dần của lũy thừa biến x ta dùng lệnh sort(f,x,ascending);
Ví dụ: sort(x^3+a^2*x-x^2+5*x+x^4-9*b*x^2, x, ascending);
5.11. Sắp xếp đa thức theo chiều giảm dần lũy thừa của biến
Để sắp xếp đa thức f theo chiều tăng dần của lũy thừa biến x ta dùng lệnh sort(f,x, descending);
Ví dụ: sort(x^3+a^2*x-x^2+5*x+x^4-9*b*x^2, x, descending);
#6. Đồ thị hàm số
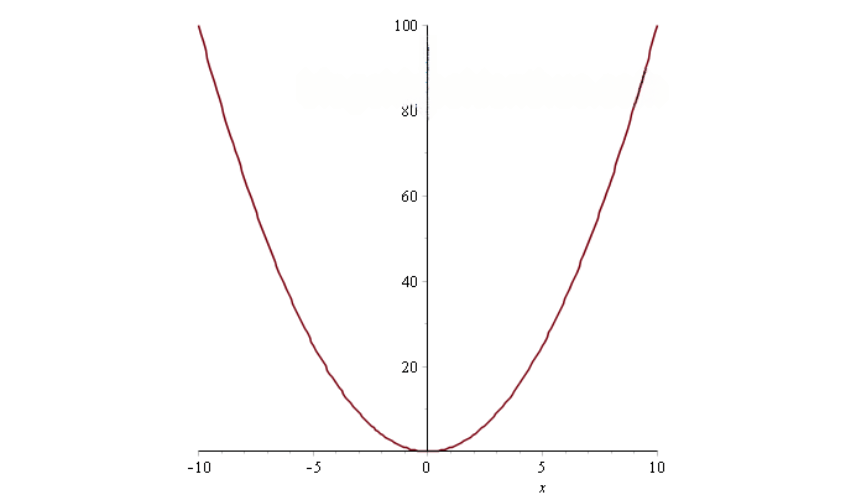
Để vẽ đồ thị hàm số y=f(x) với x thuộc [a,b] ta dùng lệnh plot(f(x),x=a..b);
plot(x^2,x=-10..10);
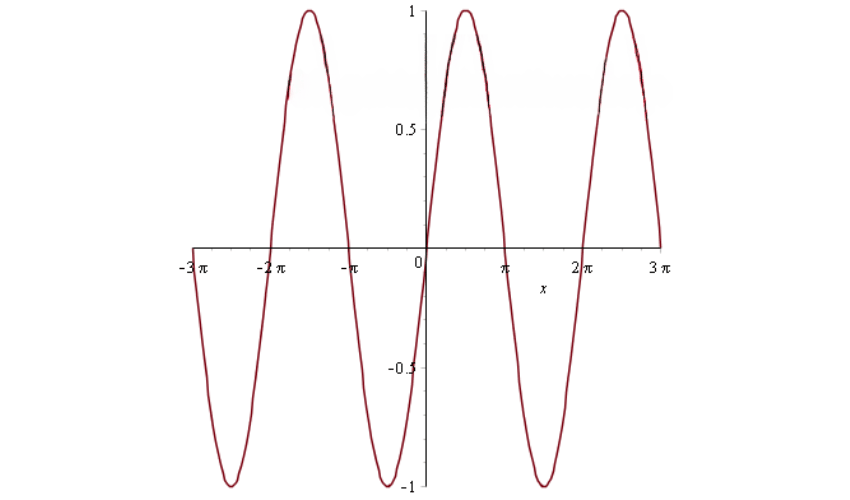
plot(sin(x),x=-3*Pi..3*Pi);
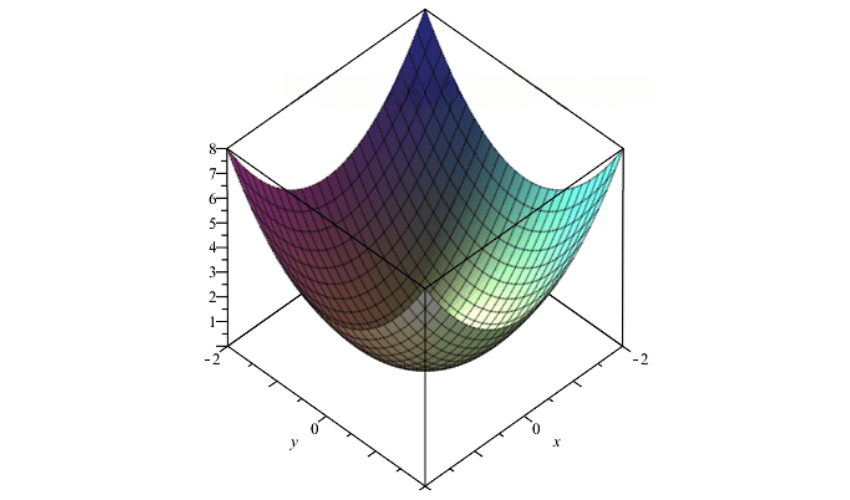
Để vẽ đồ thị hàm số z=f(x,y) trong không gian với x thuộc [a,b] và y thuộc [c,d] ta dùng lệnh plot3d(f(x),x=a..b,y=c..d);
Ví dụ: plot3d(x^2+y^2, x = -2 .. 2, y = -2 .. 2);
V. Các phép tính giải tích trong Maple
#1. Phép tính giới hạn
Để tính giới hạn của một biểu thức f ta dùng lệnh limit(f, x = a, ch);
Trong đó:
- f là biểu thức đại số.
- x là đối số chọn lấy giới hạn.
- a là điểm giới hạn.
- ch có thể chọn một trong bốn loại left, right, real, complex.
y:=tan(x)/tan(3*x);
limit(y,x=Pi/2);
#2. Phép tính đạo hàm
Để tính đạo hàm của một biểu thức ta dùng lệnh diff(f, x1, x2, …, xn);
Trong đó:
- f là biểu thức đại số.
- x1, x2,…,xn là tên của các tham số.
Ví dụ: diff(x^2+sqrt(x+1),x);
#3. Phép tính tích phân xác định và không xác định
Để tính tích phân không xác định ta dùng lệnh int(biểu thức, x);
Để tính tích phân xác định ta dùng lệnh int(biểu thức, x=a..b,…);
Trong đó:
- x là tên đối số lấy tích phân
- a, b là khoảng lấy tích phân
- …là các tùy chọn khác
Ví dụ: int((2*x^2-3*x+1)/(x^3-1), x);
VI. Lời kết
Qua bài viết này, Thủ Thuật Hack đã trình bày hầu hết các lệnh thường dùng để giải các dạng bài toán phổ biến trong chương trình Trung học. Mỗi lệnh đều được kèm theo cú pháp và ví dụ minh họa dễ hiểu.
Tuy nhiên, trong thực tế, để giải quyết một bài toán, bạn cần thực hiện liên tiếp và theo thứ tự các lệnh.
Chẳng hạn, để tính diện tích của hình phẳng được giới hạn bởi hai hàm số, bạn cần thực hiện các lệnh sau: đầu tiên là lệnh giải phương trình `solve;`, tiếp theo là lệnh vẽ đồ thị `plot;`, và cuối cùng là lệnh tính tích phân `int;`.
Để thuận tiện cho việc học và thực hành, bạn có thể tải tệp tin bài tập tại đây. Tệp tin này có định dạng *.mw của chương trình Maple, rất tiện lợi để thực hành trực tiếp.



